Assignment 1

Estimating means and standard deviations

Before completing this assignment, please read the brms walkthrough.

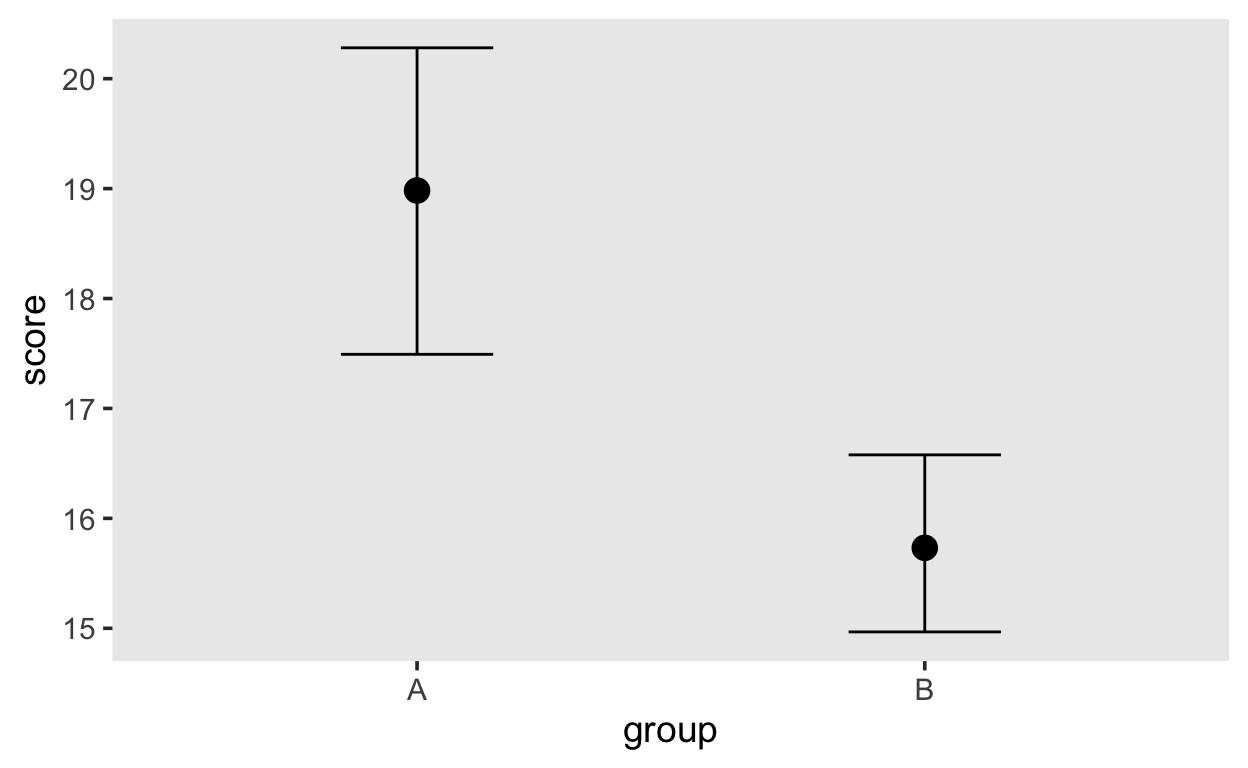
We fitted a gaussian model to some simple generated data. However, in the model we assumed that both groups had the same standard deviations. This assumption is not really necessary, however, as we can easily fit a model in which we allow both mean and standard deviation to vary between groups.

library(tidyverse)
library(brms)

theme_set(theme_grey(base_size = 14) +
            theme(panel.grid = element_blank()))

Generate data

N <- 10

mean_a <- 20.0
sigma_a <- 2.0

mean_b <- 16.0
sigma_b <- 1.5

set.seed(12)
d <- tibble(A = rnorm(N, mean_a, sigma_a),
            B = rnorm(N, mean_b, sigma_b))
d <- d |>
  pivot_longer(everything(), names_to = "group",
                values_to = "score") |> 
  mutate(group = as_factor(group)) |> 
  arrange(group)

brms allows us easily fit both the main parameter (in this case the mean), as well as further distributional parameters. We simply need to wrap the formula in the bf() function. Therefore, instead of the formula score ~ group we can use this bf(score ~ group, sigma ~ group).

score ~ group

Can be replaced with:

bf(score ~ group, sigma ~ group)

Perform the steps described in the walkthrough, but this time for the model that allows both \(\mu\) and \(\sigma\) to vary. Does this model perform well? Are you able to recover the true parameter values?

NOTE: The standard deviation must be positive; therefore we are predicting log(sigma) with our linear predictor. To recover the parameter on the original scale, you need to use the inverse function, which is the exponential function exp().

Try it out; if you get stuck, you can always ask questions on Zulip.

Show code

get_prior(bf(score ~ group, sigma ~ group),
          data = d)

                   prior     class   coef group resp  dpar nlpar
                  (flat)         b                              
                  (flat)         b groupB                       
 student_t(3, 16.9, 2.5) Intercept                              
                  (flat)         b                   sigma      
                  (flat)         b groupB            sigma      
    student_t(3, 0, 2.5) Intercept                   sigma      
 bound       source
            default
       (vectorized)
            default
       (vectorized)
       (vectorized)
            default

Show code

m3 <- brm(bf(score ~ group, sigma ~ group),
          prior = prior(normal(0, 4), class = b),
          data = d, 
          file = "models/m3")

Show code

conditional_effects(m3)

Show code

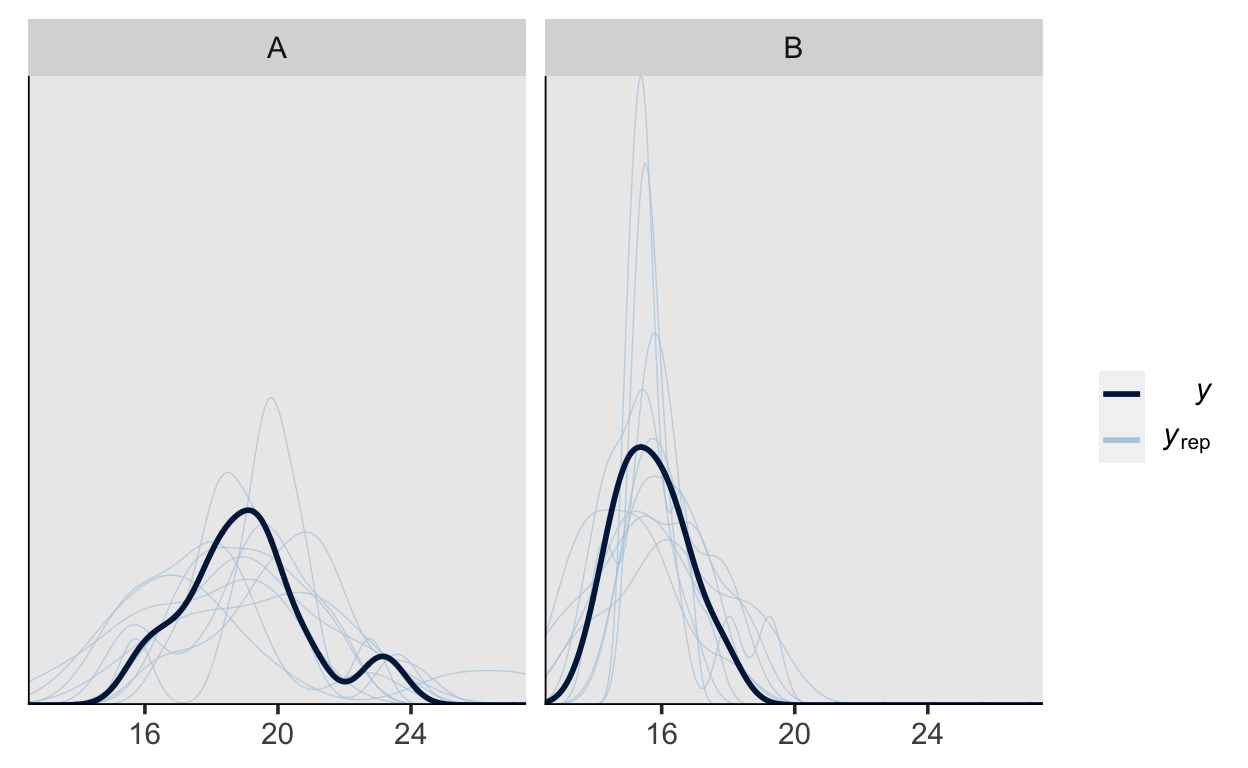
pp_check(m3)

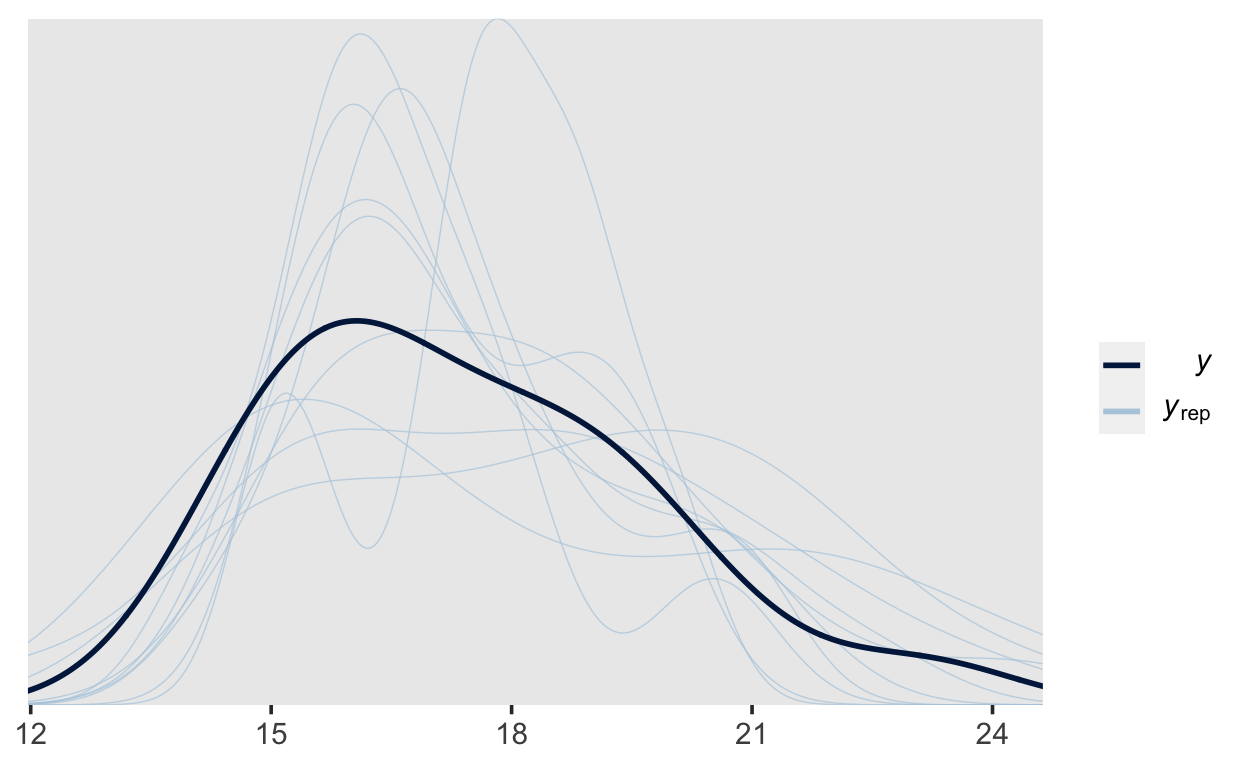
Show code

pp_check(m3, type = "dens_overlay_grouped", group = "group")