Assignment 4

Effect of tDCS stimulation on episodic memory

true
05-28-2021
Show code 
library(tidyverse)
library(brms)

theme_set(theme_grey(base_size = 14) +
            theme(panel.grid = element_blank()))

Effect of tDCS on memory

You are going to analyze data from a study in which 34 elderly subjects were given anodal (activating) tDCS over their left tempero-parietal junction (TPJ). Subjects were instructed to learn association between images and pseudo-words (data were inspired by Antonenko et al. (2019)).

Episodic memory is measured by percentage of correctly recalled word-image pairings. We also have response times for correct decisions.

Each subject was tested 5 times in the TPJ stimulation condition, and a further 5 times in a sham stimulation condition.

The variables in the dataset are:

subject: subject ID
stimulation: TPJ or sham (control)
block: block
age: age
correct: accuracy per block
rt: mean RTs for correct responses

You are mainly interested in whether recall ability is better during the TPJ stimulation condition than during sham.

Show code 
d <- read_csv("https://raw.githubusercontent.com/kogpsy/neuroscicomplab/main/data/tdcs-tpj.csv")
Show code 
glimpse(d)

Rows: 340
Columns: 6
$ subject     <dbl> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, …
$ stimulation <chr> "control", "control", "control", "control", "con…
$ block       <dbl> 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, …
$ age         <dbl> 68, 68, 68, 68, 68, 68, 68, 68, 68, 68, 67, 67, …
$ correct     <dbl> 0.8, 0.4, 0.4, 0.4, 0.6, 0.4, 0.4, 0.6, 0.6, 0.8…
$ rt          <dbl> 1.650923, 1.537246, 1.235620, 1.671189, 1.408333…
Show code 
d <- d %>% 
  mutate(across(c(subject, stimulation, block), ~as_factor(.))) %>% 
  drop_na()

  1. specify a linear model

  2. specify a null model

  3. compare models using approximate leave-one-out cross-validation

  4. estimate a Bayes factor for the effect of TPJ stimulation

    • using the Savage-Dickey density ratio test
    • using the bridge sampling method

  5. control for subjects’ age

Linear model

Show code 
fit1 <- brm(correct ~ stimulation + (stimulation| subject),
            prior = prior(normal(0, 1), class = b),
            data = d,
            file = "models/ass4-1")
Show code 
summary(fit1)

 Family: gaussian 
  Links: mu = identity; sigma = identity 
Formula: correct ~ stimulation + (stimulation | subject) 
   Data: d (Number of observations: 315) 
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Group-Level Effects: 
~subject (Number of levels: 34) 
                              Estimate Est.Error l-95% CI u-95% CI
sd(Intercept)                     0.04      0.02     0.00     0.08
sd(stimulationTPJ)                0.03      0.02     0.00     0.08
cor(Intercept,stimulationTPJ)    -0.12      0.56    -0.96     0.93
                              Rhat Bulk_ESS Tail_ESS
sd(Intercept)                 1.00     1063     1691
sd(stimulationTPJ)            1.00     1773     1704
cor(Intercept,stimulationTPJ) 1.00     2638     2093

Population-Level Effects: 
               Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
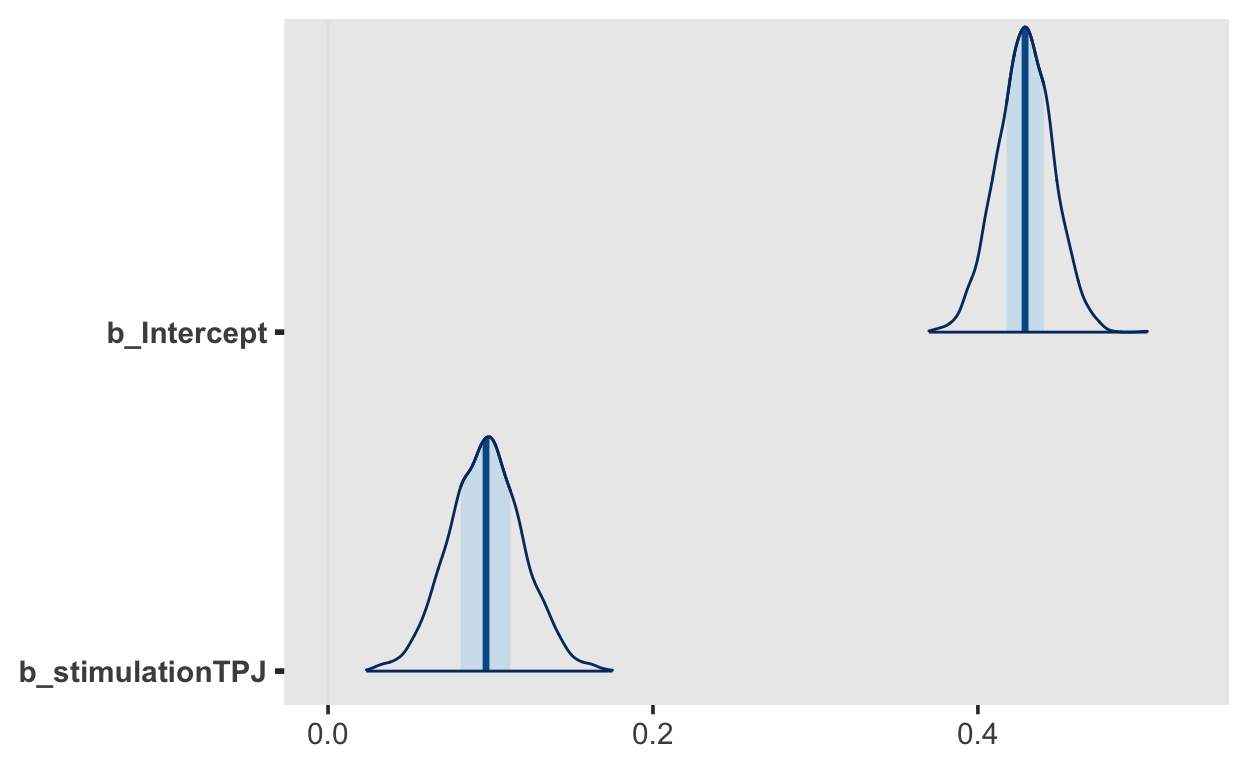
Intercept          0.43      0.02     0.39     0.46 1.00     4370
stimulationTPJ     0.10      0.02     0.05     0.14 1.00     5662
               Tail_ESS
Intercept          2819
stimulationTPJ     2553

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma     0.19      0.01     0.18     0.21 1.00     4488     2904

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
Show code 
mcmc_plot(fit1, "b_", type = "areas")

Null model

Show code 
fit2 <- brm(correct ~ 1 + (stimulation| subject),
            data = d,
            file = "models/ass4-2")

Model comparison using loo

Show code 
loo_fit_1 <- loo(fit1)
loo_fit_1


Computed from 4000 by 315 log-likelihood matrix

         Estimate   SE
elpd_loo     62.3 11.3
p_loo        14.4  1.1
looic      -124.7 22.6
------
Monte Carlo SE of elpd_loo is 0.1.

All Pareto k estimates are good (k < 0.5).
See help('pareto-k-diagnostic') for details.
Show code 
loo_fit_2 <- loo(fit2)
loo_fit_2


Computed from 4000 by 315 log-likelihood matrix

         Estimate   SE
elpd_loo     54.3 10.8
p_loo        17.0  1.3
looic      -108.5 21.7
------
Monte Carlo SE of elpd_loo is 0.1.

Pareto k diagnostic values:
                         Count Pct.    Min. n_eff
(-Inf, 0.5]   (good)     313   99.4%   1428      
 (0.5, 0.7]   (ok)         2    0.6%   1509      
   (0.7, 1]   (bad)        0    0.0%   <NA>      
   (1, Inf)   (very bad)   0    0.0%   <NA>      

All Pareto k estimates are ok (k < 0.7).
See help('pareto-k-diagnostic') for details.
Show code 
loo_compare(loo_fit_1, loo_fit_2)

     elpd_diff se_diff
fit1  0.0       0.0   
fit2 -8.1       3.7

Model comparison via Bayes factor

Show code 
fit1_bf <- brm(correct ~ stimulation + (stimulation| subject),
            prior = prior(normal(0, 1), class = b),
            data = d,
            iter = 1e4,
            save_pars = save_pars(all = TRUE),
            file = "models/ass4-bf_1")
Show code 
fit2_bf <- brm(correct ~ 1 + (stimulation| subject),
            prior = prior(normal(0, 1), class = b),
            data = d,
            iter = 1e4,
            save_pars = save_pars(all = TRUE),
            file = "models/ass4-bf_2")
Show code 
loglik_1 <- bridge_sampler(fit1_bf, silent = TRUE)
loglik_2 <- bridge_sampler(fit2_bf, silent = TRUE)
Show code 
BF_10 <- bayes_factor(loglik_1, loglik_2)
BF_10

Estimated Bayes factor in favor of x1 over x2: 116.01251

Control for age

Show code 
fit3 <- brm(correct ~ stimulation + age + (stimulation | subject),
            prior = prior(normal(0, 1), class = b),
            data = d,
            file = "models/ass4-3")
Show code 
fit3

 Family: gaussian 
  Links: mu = identity; sigma = identity 
Formula: correct ~ stimulation + age + (stimulation | subject) 
   Data: d (Number of observations: 315) 
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
         total post-warmup samples = 4000

Group-Level Effects: 
~subject (Number of levels: 34) 
                              Estimate Est.Error l-95% CI u-95% CI
sd(Intercept)                     0.03      0.02     0.00     0.07
sd(stimulationTPJ)                0.03      0.02     0.00     0.08
cor(Intercept,stimulationTPJ)    -0.07      0.56    -0.95     0.92
                              Rhat Bulk_ESS Tail_ESS
sd(Intercept)                 1.00     1066     1325
sd(stimulationTPJ)            1.00     1476     2197
cor(Intercept,stimulationTPJ) 1.00     2435     1959

Population-Level Effects: 
               Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
Intercept          0.16      0.25    -0.33     0.64 1.00     4074
stimulationTPJ     0.10      0.02     0.05     0.14 1.00     5234
age                0.00      0.00    -0.00     0.01 1.00     4075
               Tail_ESS
Intercept          2701
stimulationTPJ     2720
age                2688

Family Specific Parameters: 
      Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma     0.19      0.01     0.18     0.21 1.00     3919     2810

Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).
Show code 
loo_fit_3 <- loo(fit3)
Show code 
loo_compare(loo_fit_1, loo_fit_3)

     elpd_diff se_diff
fit1  0.0       0.0   
fit3 -0.4       1.0
Show code 
fit3_bf <- brm(correct ~ stimulation + age + (stimulation| subject),
            prior = prior(normal(0, 1), class = b),
            data = d,
            iter = 1e4,
            save_pars = save_pars(all = TRUE),
            file = "models/ass4-bf_3")
Show code 
loglik_3 <- bridge_sampler(fit3_bf, silent = TRUE)
Show code 
BF_01 <- bayes_factor(loglik_3, loglik_1)
BF_01

Estimated Bayes factor in favor of x1 over x2: 0.00668
Antonenko, Daria, Dayana Hayek, Justus Netzband, Ulrike Grittner, and Agnes Flöel. 2019. “tDCS-Induced Episodic Memory Enhancement and Its Association with Functional Network Coupling in Older Adults.” Scientific Reports 9 (1, 1): 2273. https://doi.org/10.1038/s41598-019-38630-7.

References

Corrections

If you see mistakes or want to suggest changes, please create an issue on the source repository.

Reuse

Text and figures are licensed under Creative Commons Attribution CC BY 4.0. Source code is available at https://github.com/awellis/learnmultilevelmodels, unless otherwise noted. The figures that have been reused from other sources don't fall under this license and can be recognized by a note in their caption: "Figure from ...".

Citation

For attribution, please cite this work as

Ellis (2021, May 28). Learn multilevel models: Assignment 4. Retrieved from https://awellis.github.io/learnmultilevelmodels/asssignment-4.html

BibTeX citation

@misc{ellis2021assignment,
  author = {Ellis, Andrew},
  title = {Learn multilevel models: Assignment 4},
  url = {https://awellis.github.io/learnmultilevelmodels/asssignment-4.html},
  year = {2021}
}