library(kableExtra)
library(viridis)
library(tidyverse)
library(brms)
# set ggplot theme
theme_set(theme_grey(base_size = 14) +
theme(panel.grid = element_blank()))
# set rstan options
rstan::rstan_options(auto_write = TRUE)
options(mc.cores = 4)
Check out this interactive web app for response time distributions (Lindeløv 2021).
We will try to fit a distributin that is appropriate for response times to data from Wagenmakers and Brown (2007).
Subjects performed a lexical decision task in two conditions (speed stress / accuracy stress). We will look at conly correct responses.
library(rtdists)
data(speed_acc)
speed_acc <- speed_acc %>%
as_tibble()
df_speed_acc <- speed_acc %>%
# remove rts under 180 ms and over 3 sec
filter(rt > 0.18, rt < 3) %>%
# convert to char
mutate(across(c(stim_cat, response), as.character)) %>%
# Kcorrect responses
filter(response != 'error', stim_cat == response) %>%
# convert back to factor
mutate(across(c(stim_cat, response), as_factor))
df_speed_acc
# A tibble: 27,936 x 9
id block condition stim stim_cat frequency response rt
<fct> <fct> <fct> <fct> <fct> <fct> <fct> <dbl>
1 1 1 speed 5015 nonword nw_low nonword 0.7
2 1 1 speed 6481 nonword nw_very_low nonword 0.46
3 1 1 speed 3305 word very_low word 0.455
4 1 1 speed 4468 nonword nw_high nonword 0.773
5 1 1 speed 1047 word high word 0.39
6 1 1 speed 5036 nonword nw_low nonword 0.603
7 1 1 speed 1111 word high word 0.435
8 1 1 speed 6561 nonword nw_very_low nonword 0.524
9 1 1 speed 1670 word high word 0.427
10 1 1 speed 6207 nonword nw_very_low nonword 0.456
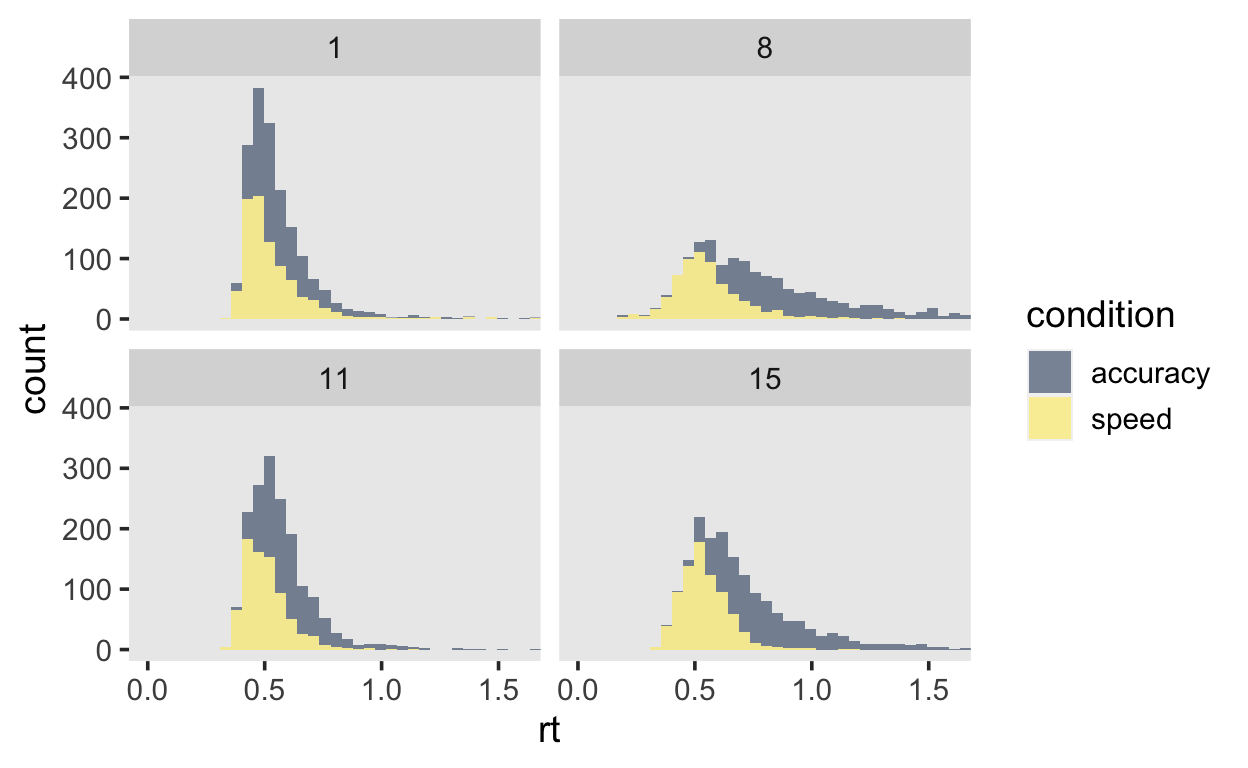
# … with 27,926 more rows, and 1 more variable: censor <lgl>Plot a few subjects to get an overview.
data_plot <- df_speed_acc %>%
filter(id %in% c(1, 8, 11, 15))
data_plot %>%
ggplot(aes(x = rt)) +
geom_histogram(aes(fill = condition), alpha = 0.5, bins = 60) +
facet_wrap(~id) +
coord_cartesian(xlim=c(0, 1.6)) +
scale_fill_viridis(discrete = TRUE, option = "E")
Shifted Lognormal
We’ll not try to fit a shifted-lognormal distribution
The density is given by:
\[ f(x) = \frac{1} {(x - \theta)\sigma\sqrt{2\pi}} exp\left[ -\frac{1}{2} \left(\frac{ln(x - \theta) - \mu }{\sigma} \right)^2 \right] \]
m\(\mu\), \(\sigma\) und \(\theta\) are the three parameters. \(\theta\) shifts the entire distribition along the x axis. \(\mu\) and \(\sigma\) have an effect on the shape.
\(\mu\) is often interpreted as a difficulty parameter. Both median and mean depend on \(\mu\)
The median is given by \(\theta + exp(\mu)\).
\(\sigma\) is the scale parameter (standard deviation); It affects the mean, but not the median.
The mean is \(\theta + exp\left( \mu + \frac{1}{2}\sigma^2\right)\)
We are mainly interested in the \(\mu\) parameter.
When fitting with brms, we need to be aware that \(\mu\) and \(\sigma\) are on the log scale.
\[ y_i \sim Shifted Lognormal(\mu, \sigma, \theta) \]
\[ log(\mu) = b_0 + b_1 X_1 + ...\] Both \(\sigma\) and \(\theta\) may also be predicted, or simply estimated.
\[ \sigma \sim Dist(...) \]
\[ \theta \sim Dist(...) \]
priors <- get_prior(rt ~ condition + (1|id),
family = shifted_lognormal(),
data = df_speed_acc)
priors %>%
as_tibble() %>%
select(1:4)
# A tibble: 8 x 4
prior class coef group
<chr> <chr> <chr> <chr>
1 "" b "" ""
2 "" b "conditionspeed" ""
3 "student_t(3, -0.6, 2.5)" Intercept "" ""
4 "uniform(0, min_Y)" ndt "" ""
5 "student_t(3, 0, 2.5)" sd "" ""
6 "" sd "" "id"
7 "" sd "Intercept" "id"
8 "student_t(3, 0, 2.5)" sigma "" "" priors <- prior(normal(0, 0.1), class = b)
m1 <- brm(rt ~ condition + (1|id),
family = shifted_lognormal(),
prior = priors,
data = df_speed_acc,
file = 'models/m1_shiftedlognorm')
summary(m1)
Family: shifted_lognormal
Links: mu = identity; sigma = identity; ndt = identity
Formula: rt ~ condition + (1 | id)
Data: df_speed_acc (Number of observations: 27936)
Samples: 4 chains, each with iter = 2000; warmup = 1000; thin = 1;
total post-warmup samples = 4000
Group-Level Effects:
~id (Number of levels: 17)
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
sd(Intercept) 0.15 0.03 0.11 0.23 1.01 467
Tail_ESS
sd(Intercept) 736
Population-Level Effects:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS
Intercept -0.68 0.04 -0.76 -0.61 1.01 455
conditionspeed -0.40 0.00 -0.41 -0.39 1.00 1766
Tail_ESS
Intercept 594
conditionspeed 1707
Family Specific Parameters:
Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
sigma 0.37 0.00 0.36 0.37 1.00 1863 2071
ndt 0.17 0.00 0.17 0.18 1.00 1479 2166
Samples were drawn using sampling(NUTS). For each parameter, Bulk_ESS
and Tail_ESS are effective sample size measures, and Rhat is the potential
scale reduction factor on split chains (at convergence, Rhat = 1).# intial values for expected ndt
inits <- function() {
list(Intercept_ndt = -1.7)
}
m2 <- brm(bf(rt ~ condition + (1|id),
ndt ~ 1 + (1|id)),
family = shifted_lognormal(),
prior = priors,
data = df_speed_acc,
inits = inits,
init_r = 0.05,
control = list(max_treedepth = 12),
file = 'models/m2_shiftedlognorm_ndt')
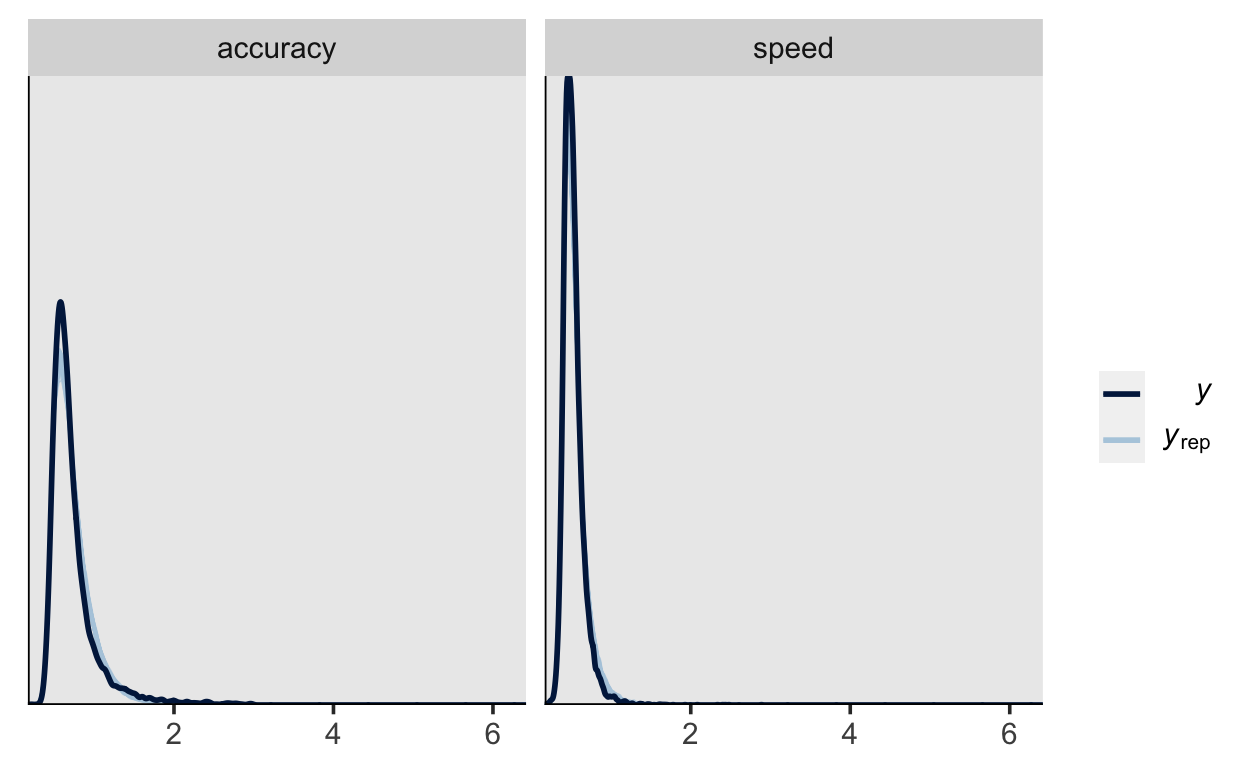
pp_check(m2,
type = "dens_overlay_grouped",
group = "condition",
nsamples = 200)